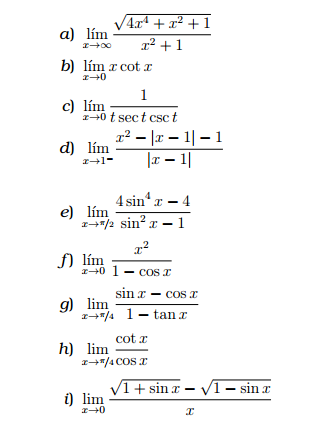Saltar la navegación

5. EJERCICIOS

1)  Evalúe los siguientes límites, y establezca si existen o no.

                       

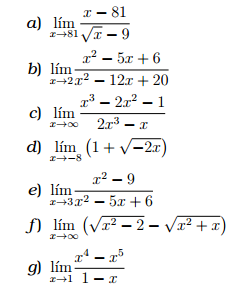
2)  Para las funciones dadas encuentre el límite:

                     

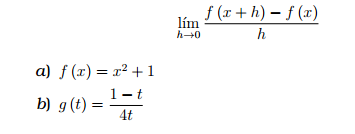
3) Evalúe los siguientes límites o establezca que no existen

  1.      

4)   Haga la gráfica de la función dada y determine el valor de x para el cual ella puede ser discontinua, además, determine si la función efectivamente, es o no discontinua en ese valor.

      
 

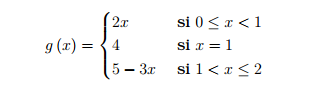
5)  Con la gráfica de la función dada, determine:

    

6. Halle los valores de m y n para que la función sea continua

                 

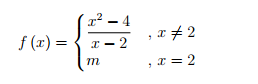
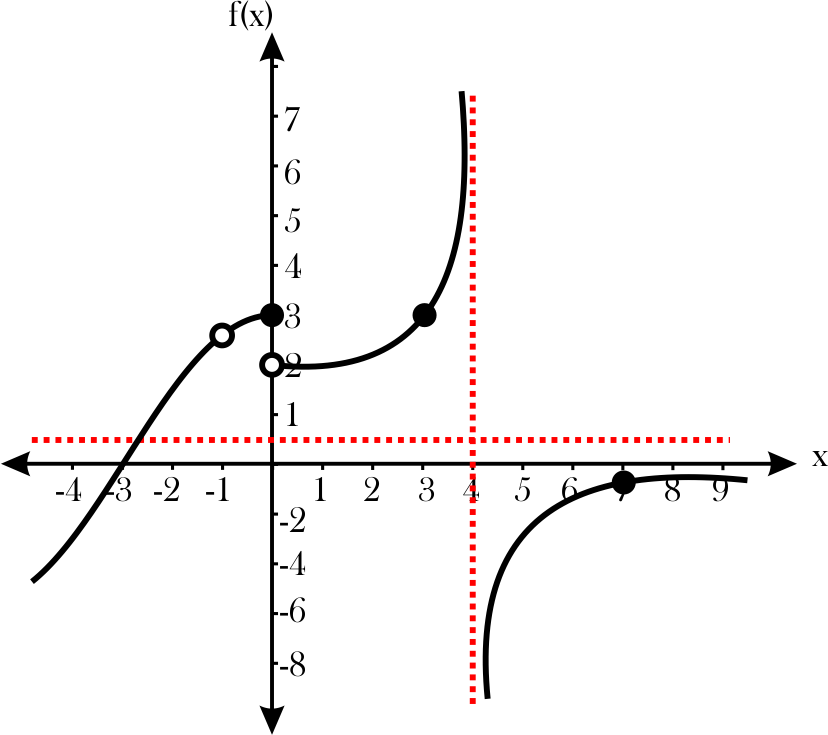
7)  Describa la gráfica dada, utilice conceptos matemáticos, enuncie 10 aspectos que den cuenta de: Continuidad, límites, límites laterales, al infinito e infinitos.

figure Imagenes/Grafica_141.png
8) Esboce la gráfica de las funciones dadas, utilizando todos los criterios vistos: asíntotas verticales y horizontales, ceros de la función, valores extremos (máximos y mínimos), intervalos de crecimiento y decrecimiento, criterio de la primera derivada, intervalos de concavidad hacia arriba y concavidad hacia abajo, criterio de la segunda derivada, puntos de inflexión
    • f(x) = x2 + 2x − 1
    • g(t) = sen  t
    • h(x) = (1 − x)  / ( x − 2)
    • f(t) = (x − 3)2   /   (x2 − 4)

9) Ejercicios de Aplicación de valores máximos y mínimos

  • Una fábrica de cajas de cartón para regalo, tiene disponibles, cartones de 15 × 12 cms. El diseño de la caja, implica cortar cuadrados en cada una de las esquinas, y doblando los lados. Encuentre la longitud requerida para el lado del cuadrado a cortar si se desean tener las cajitas de máximo volumen
  • Encuentre el número en el intervalo cerrado [0, 2], tal que la diferencia entre dicho número y su cuadrado sea máximo.
  • Un islote está ubicado en un punto A, 5Km mar adentro del punto más cercano B, en una playa recta. Una persona se encuentra en el islote y desea ir hacia el punto C, 9Km playa debajo de B. La persona entonces puede alquilar un bote por $15.000 el kilómetro y viajar por agua hacia y un punto P, entre B y C, y de ahí rentar un coche, cuyo alquiler cuesta $10.000 pesos por kilómetro y recorrer el camino restante de P a C. Encuentre la ruta más económica para ir del punto A al punto C.

Obra publicada con Licencia de Documentación Libre de GNU (GNU Free Documentation License) (Versión local)