Definición intuitiva
La expresión limx → af(x) = L, significa que cuando la x está muy próxima (por izquierda y por derecha) al valor “a”, la función está muy próxima a valer L, esto es: limx → af(x) = L
La notación para los ejemplos dados queda de la siguiente manera:

En lo que se sigue de este curso, se indicará (como se tiene establecido en toda literatura) que los límites laterales se denotan de la siguiente manera: limx → a − f(x): Límite de la función f, cuando x tiende a a por izquierda.
limx → a + f(x) : Límite de la función f, cuando x tiende a a por derecha.
¿Pero cómo evaluar límites sin ayuda de tabla de valores. ¿De qué otra forma se puede encontrar el valor de -4, en el ejemplo 1, el valor de cero en el ejemplo 2?.
Note que en el primer caso se puede factorizar y luego simplificar y después sustituir; en el segundo caso, se sustituye directamente. A continuación, se trabajaran límites utilizando procedimientos algebraicos (factorizar, racionalizar, completar cuadrados, etc).
Ejemplo
A continuación se resuelven algunos límites.

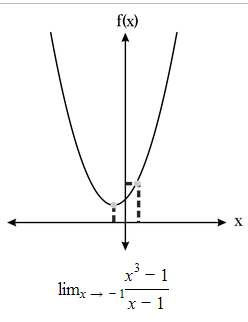
Figura 1


Figura 2 f(x) = √x + 1

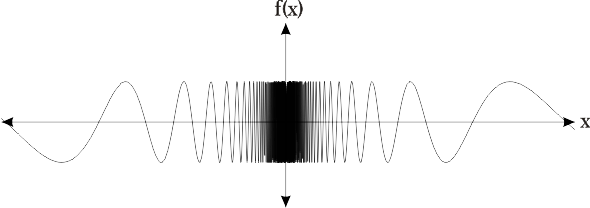
Figura 3 f(x) = sin(1x)
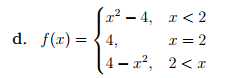

Figura 4 Gráfica del ejemplo d

Como los límites laterales son iguales a cero, entonces el límite inicial propuesto existe y es cero.


Figura 5 Función del ejemplo e
Obra publicada con Licencia de Documentación Libre de GNU (GNU Free Documentation License) (Versión local)