Saltar la navegación

Límites

Definición

En ésta Unidad se dan las dos definiciones de límites, intuitiva y rigurosa. Primero la intuitiva, para que el estudiante se apoye en la misma y empiece a apropiarse del concepto del límite como el único valor al cual se acerca una función cuando su variable independiente, está muy próxima a tomar un valor específico.

 El estudio de límites requiere en cualquier estudiante el manejo del álgebra, toda vez que para resolver un gran número de ejercicios de límites se requieren de la manipulación algebraica o trigonométrica de las expresiones involucradas. 
 
  Se empieza con la idea intuitiva de límite de una función, luego se trabaja con la definición rigurosa del mismo, seguido de los límites infinitos y al infinito, y finalmente, la presencia de asíntotas de una función y su relación con los límites.
 En esta unidad cada estudiante puede poner a prueba sus conocimientos en los temas aquí tratados, con el link:
http://temasmatematicos.uniandes.edu.co/límites/.
A continuación se ilustra la idea intuitiva del límite de una función en un valor cualquiera de su variable independiente, con ayuda de una tabla de valores.
Posteriormente, se trabajará la idea intuitiva con procesos algebraicos y finalmente, se estudiará la definición rigurosa del límite.

Dada la función

                                              

¿A qué valor tiende ella cuando x está muy cerca a tomar el valor de -2?. La tabla 1 ilustra lo que sucede en la función dada.

x f(x)
-2,1 -4,1
-2,01 -4,01
-2,001 -4,001
-2 No definida
-1,999 -3,999
-1,99 -3,99
-1,9 -3,9
Tabla 1   

Note que la función tiende a  − 4, cuando x tiende a  − 2 por izquierda y por derecha, aunque la función no está definida en x =  − 2.

figure Imagenes/Grafica_83.png
Figura 1 f(x) = (x2 − 4)  /  (x + 2)
  1. f(x) = x2 + 5x ¿Qué pasa con la función cuando x tiende a 0? La tabla 2 muestra el comportamiento de la función.
    x f(x)
    -0,1 -0,49
    -0,01 -0,0501
    -0,001 -0,005001
    0 0
    0,001 0,005001
    0,01 0,0501
    0,1 0,49
    Tabla 2
    Se observa que la función tiende a cero, tanto por izquierda como por derecha.
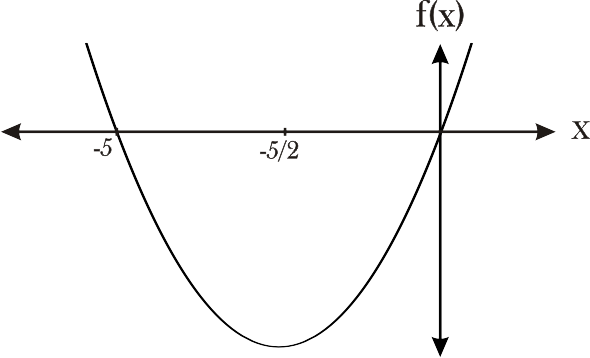
figure Imagenes/Grafica_84.png
Figura 2 f(x) = x2 + 5x
     2.  Dada la función f(x) = 1 / x2, ¿Cuándo x tiende a cero, qué pasa con la función? La tabla 3 ilustra lo que sucede en este caso.
  1. x f(x)
    -0,1 100
    -0,01 10000
    -0,001 1000000
    0 No definida
    0,001 1000000
    0,01 10000
    0,1 100
    Tabla 3

La tabla de valores muestra que la función dada no tiende a un valor, sino que crece indefinidamente. 
En los ejemplos 1 y 2, se puede decir que la función tiende a un único valor cuando la variable independiente tiende a un valor específico, esto se denota con la siguiente expresión:
limx → af(x) = L.
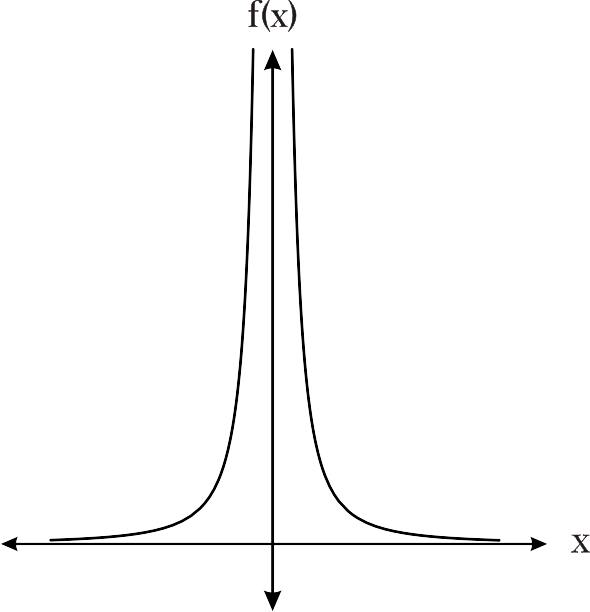
figure Imagenes/Grafica_85.png
Figura 3 f(x) = 1 / x2.

Obra publicada con Licencia de Documentación Libre de GNU (GNU Free Documentation License) (Versión local)