Límites infinitos y al infinito
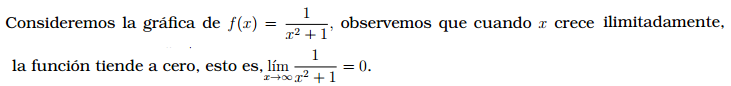
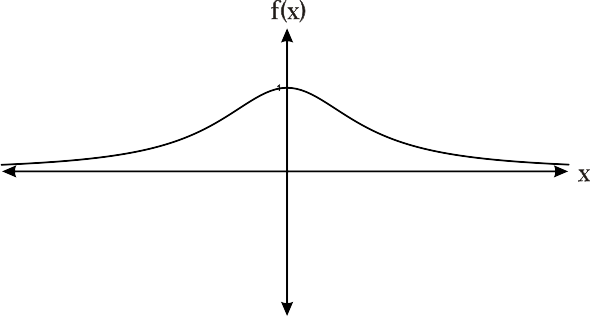
Figura 1 f(x) = 1 / (x2 + 1)
Note que para esta función la recta y = 0 es una asíntota horizontal
Definición
Sea f una función definida en [c, ∞) para un c ∈ ℝ, entonces si
Significa:
∀ ε > 0, ∃ M ∈ ℝ tal que si x > M entonces |f(x) − 1| < ε.
Evaluar los siguientes límites:
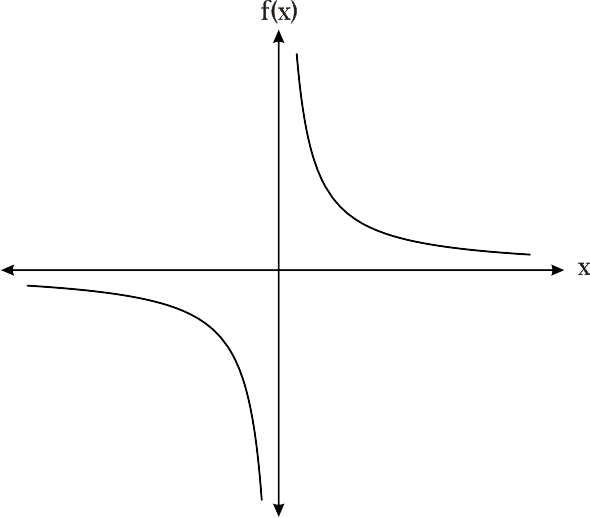Figura 2 f(x) = 1 / x
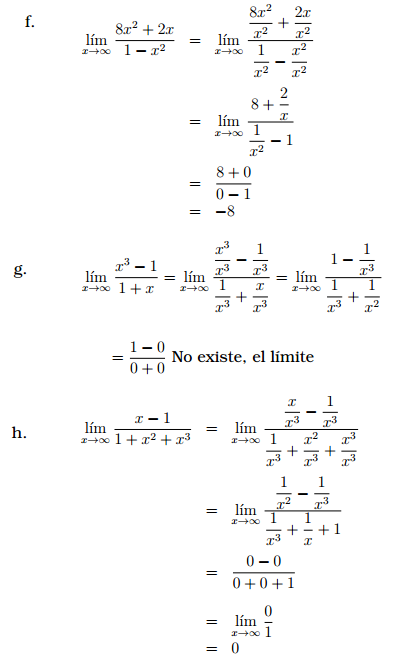
Propiedades de los Límites al Infinito de Funciones Racionales
[a] Existe y es 0 (cero) si grado p(x) es menor que el grado de q(x).
[b] Existe y es igual al cociente de los coeficientes de mayor exponente si grado de p(x) = grado q(x).
[c] No existe si grado de p(x) es mayor que el grado de q(x)
Asíntotas Horizontales
Limites infinitos: Note que los siguientes límites no existen.
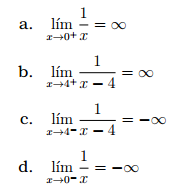
Asíntotas Verticales
Si limx → cf(x) = ±∞ , entonces x = c es una asíntota vertical a la curva de la función.
En el ejemplo c, x = 0 y x = 4 son asíntotas verticales para las funciones correspondientes.
Obra publicada con Licencia de Documentación Libre de GNU (GNU Free Documentation License) (Versión local)