Teorema de Bolzano.
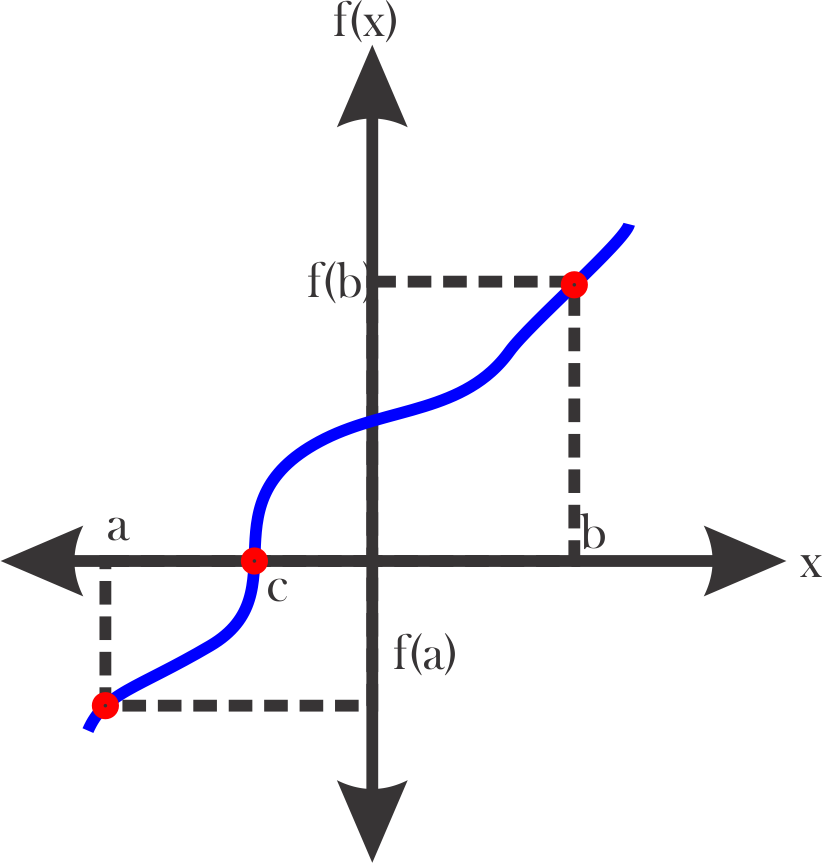
Figura 1. f(a) y f(b) de signos opuestos
Sea f una función continua en [a, b] con f(a) y f(b) de signos opuestos, entonces existe por lo menos un c ∈ ℝ; c ∈ (a, b) tal que f(c) = 0
En otras palabras, este teorema establece que si la función, es continua en [a, b] y la función evaluada en los valores extremos de ese intervalo tiene signos diferentes, entonces la curva debe cruzar el eje x, al menos una vez.

Obra publicada con Licencia de Documentación Libre de GNU (GNU Free Documentation License) (Versión local)