Teorema del valor intermedio
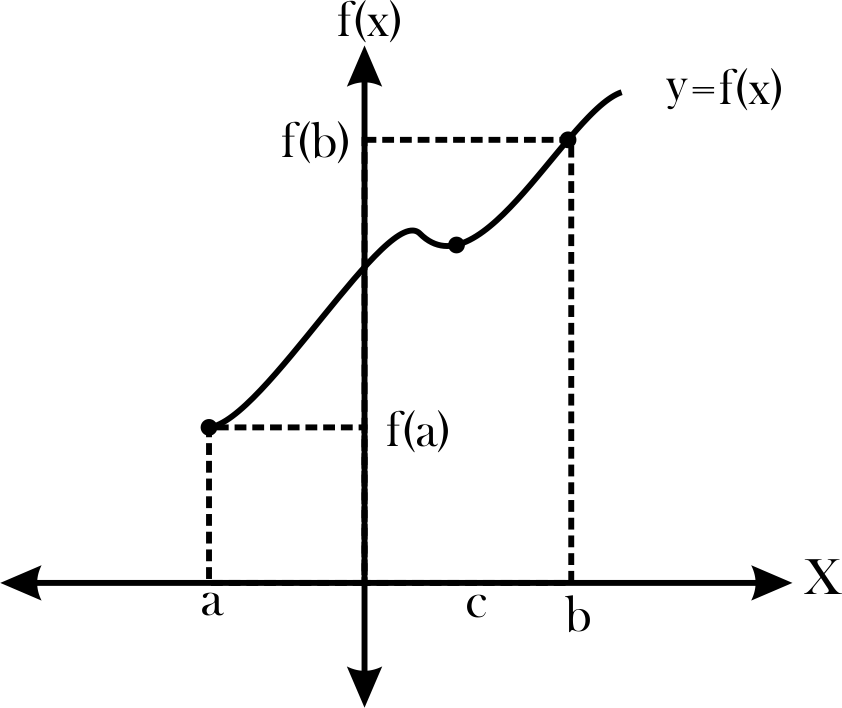
Figura 1 Teorema del Valor Intermedio
Sea f una función continua en [a, b] con f(a) ≠ f(b) y k es un valor comprendido entre f(a) y f(b), esto es, f(a) ≤ k ≤ f(b), entonces existe un c ∈ ℝ, tal que f(c) = k y c ∈ (a, b).
En otras palabras, este teorema establece que una función continua en [a, b] , toma por lo menos una vez, todos los valores comprendidos entre f(a) y f(b)
Ejemplo.


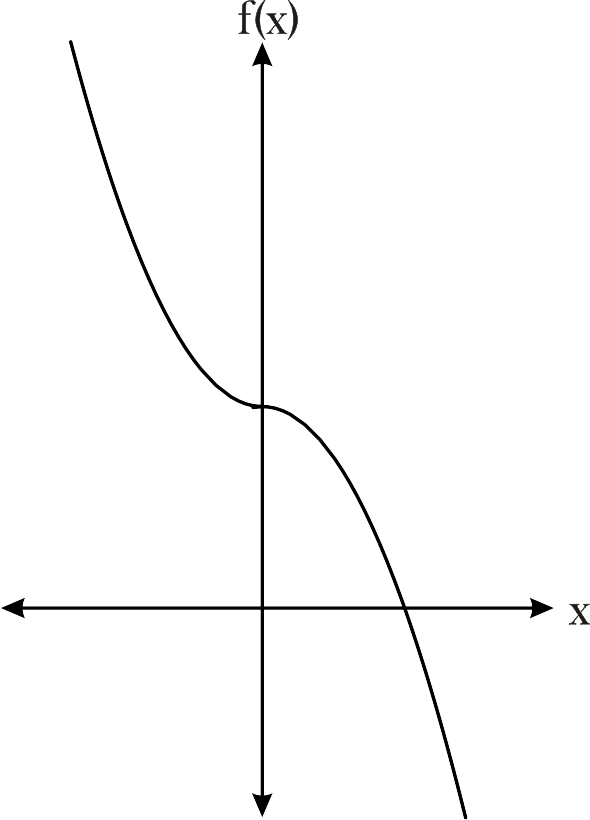
Figura 2 Gráfico del ejemplo
Obra publicada con Licencia de Documentación Libre de GNU (GNU Free Documentation License) (Versión local)