7.1 ¿Cómo encontrar la recta de regresión?
Para encontrar la recta de regresión que mejor ajuste el conjunto de datos se utiliza el Método de Mínimos Cuadrado, el cual se explicará a continuación.
Como se dijo en la sección anterior, para los n-datos de estudio, se tienen n-componentes (xi, yi), i = 1, 2, ..., n. Estas observaciones serán registradas para mayor facilidad de uso, en una tabla como se ilustra en la tabla 16.
Tabla 16
| Observación |
Xi |
Yi |
| 1 |
x1 |
y1 |
| 2 |
x2 |
y2 |
| 3 |
x3 |
y3 |
| ... |
... |
... |
| ... |
... |
... |
| n |
xn |
yn |
Lo primero que debe hacerse es identificar cual de las variables depende de la otra, identificar la variable independiente y la variable dependiente, las cuales suelen denominarse como X e Y, respectivamente. Seguidamente, se determina si existe o no una relación lineal entre las variables, para lo cual se cálcula el valor de ρ y generalmente se corrobora con el diagrama de dispersión. De esta manera, quedara un gráfico como el anterior. Renombremos las distancias di = i = 1, 2, ..., n, como ei, i = 1, 2, ..., n, valido, por que lo que hacemos en realidad es cometer un error, al aproximar cada punto con la recta que mejor los ajustes a todos, por esta razón, la ecuación que cada punto satisface es dada por.
Yi = A ⌢Xi + B + ei, i = 1, 2, ..., n. (1)
donde, los ei, i = 1, 2, ..., n, representan los errores cometidos con la aproximación, mas exactamente, representa la distancia dide cada punto a la recta. Los n-puntos generan el siguiente sistema de ecuaciones lineales

El método de Mínimos Cuadrados consiste en encontrar los valores de las constantes A y B de tal manera que se logre minimizar la suma de los cuadrados de los errores. Por razón, lo primero que se hace es despejar los eide la ecuación (1).
Ahora, la suma de los cuadrados de los errores (distancias), la denotaremos como:

Consideremos ahora, d como una función de dos variables A y B, por lo que pasa minimizar esta función se debe derivar parcialmente con respecto a cada una de estas variables para encontrar mínimos absolutos.
La derivada parcial con respecto a la variable A es dada por:
(8.1)

La derivada parcial con respecto a la variable B es dada por:
(8.2)

Al igualar a cero (2) y (3), se obtiene dos ecuaciones dos ecuaciones simultáneas para A y B:
(8.3)

(8.4)

Al resolver la ecuación (5) para B, se obtiene:
(8.5)

Al sustituir (6) en la ecuación (4) se tiene que:
(8.6)

de esta manera, se tiene que B es:
(8.7)

Con ayuda del cálculo, más exactamente con segunda derivada de d se logra mostrar que en estos valores de A y B, la función d tiene un mínimo absoluto.
Otra forma para calcular el valor de B es dado por: B = Y − AX.
El coeficiente de determinación permite cuantificar, en porcentaje, el grado de variación de la variable Y debido a la variación de la variable X.
| PROBLEMA |
SOLUCION |
Ejemplo 3
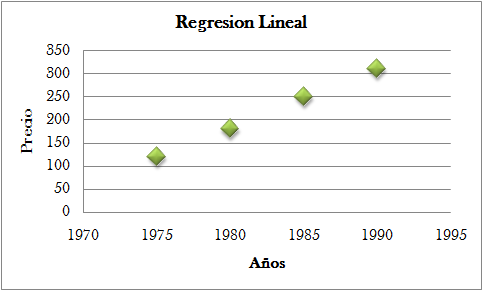
En 1975 se compro un objeto antiguo y raro por $120.000, su valor en 1980 fue de $180.000, en 1985 su precio ascendió a $250.000 y en 1990 estuvo valorizado en $310.000. Utilice el modelo de regresión lineal, para determinar el precio del artículo en el año 1995, de acuerdo al mismo patrón. ¿En qué año el articulo tendrá un valor de $471000? |
La siguiente tabla (17) muestra la información dada.
Y la ilustración 15 muestra el gráfico de dispersión.
|
Tabla 17
| Año |
0 |
1 |
2 |
3 |
| Valor (miles) |
120 |
180 |
250 |
310 |
Ilustración 15: Gráfico de dispersión para ejemplo 2
Calculando el coeficiente de correlación, se tiene que ρ = 0, 9995; por lo cual se concluye que hay entre las variables año y precio, existe una relación lineal directa, esto es, a medida que pasan los años, el artículo aumenta de precio. Ahora, para calcular el modelo de regresión lineal \overset⌢Y = A\overset⌢X + B, se requiere conocer los valores de las constantes A y B, para esto bien podemos utilizar las ecuaciones (7) y (8), o también utilizar la calculadora científica que afortunadamente, trae la opción de calcular estos valores. Primero utilizaremos las ecuaciones dadas y luego se explicara como efectuar los cálculos en la calculadora.
Como ∑4i = 1xi = 6, ∑4i = 1yi = 8600, ∑4i = 1x2i = 14 y ∑4i = 1xiyi = 16100, entonces,


De esta manera, la ecuación de regresión es dada por: ⌢Y = 640(⌢X + 1190).
Reemplazando el valor de 1995 en la variable X, se tiene: ⌢Y = 640(4) + 1190 = 375. Esto significa que para el cuarto año, es decir, en 1995 el artículo tuvo un precio de $375.000 pesos.
Note que para averiguar en qué año el articulo valdrá $471.000, se requiere despejar la variable X de la ecuación ⌢Y = 640(⌢X + 1190). Así ⌢X = ⌢Y − 1190640 = 471 − 1190640 = 5, 5. Esto significa que a mediados del año 2000, el artículo tendrá un valor de $471.000.
El coeficiente de correlación es R2 = 0.99 y este valor indica que el precio del artículo depende en un 99.99% de los años transcurridos.
Ejercicios.
1. Unos grandes almacenes obtienen los datos relacionados en la tabla 18, los cuales corresponden al número de vendedores x con el monto de ventas anuales y.
Tabla 18
| N° de vendedores |
5 |
6 |
7 |
8 |
9 |
10 |
| Ventas anuales |
2.3 |
3.2 |
4.1 |
5 |
6.1 |
7.2 |
Se supone que existe una relación lineal entre el N° de vendedores y valor de ventas anuales.
Encuentre la recta y = mx que mejor se ajusta a las mediciones anteriores. Calcule cuál sería el valor de ventas anuales si hubiese 14 vendedores.
2. Un automóvil modelo 1991 fue vendido en 1992 por $19’500000, su valor en 1993 fue 17’900000, para el 94 el valor decayó a 17’100000 y finalmente para el 95 el precio del carro era de 17’200000. Elabore el diagrama de dispersión y utilice el método de los mínimos cuadrados para hallar la recta de la regresión que mejor ajuste los datos y grafíquela junto al diagrama de dispersión, determine igualmente el precio del carro para el año 97.
3. La tabla 19 tiene la información de un comerciante, que llevo a cabo un estudio para determinar la relación entre los gastos de publicidad semanal x en miles de pesos y las ventas semanales y en miles de pesos.
Tabla 19
| Costos de publicidad |
40 |
20 |
25 |
30 |
50 |
40 |
| Ventas |
385 |
400 |
395 |
475 |
440 |
490 |
Elabore el diagrama de dispersión, encuentre la recta y = A + Bx que mejor se ajuste a estos datos y grafíquela junto al diagrama de dispersión y estime las ventas semanales cuando los gastos de publicidad ascienden a $35.000. Además de la interpretación para cuando las ventas sean nulas. ¿Cuánto habrá invertido en publicidad el comerciante si las ventas fueron $465.000?
4. Una pequeña empresa que produce artículos en guadua, ha recolectado información sobre el tiempo (en horas) que le toma a un nuevo empleado elaborar un artículo especifico, dependiendo de las semanas de experiencia que tenga el empleado. La tabla 20, contiene esta información.
Tabla 20
| Semanas |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
| Tiempo |
5 |
4 |
5 |
3 |
4 |
3.1 |
2.9 |
3 |
3 |
Con base en esta información, determine la ecuación de regresión, calcule e interprete el coeficiente de determinación, determine el tiempo requerido por un empleado que tenga solo 3 semanas de experiencia, determine cuántas semanas de experiencia tiene un empleado que elabore el artículo en 4 horas. ¿Con base en la información de la tabla, que se espera que sea el tiempo mínimo que un empleado experto se gaste en la elaboración del producto? Con base en la ecuación de regresión ¿Cuánto tiempo empleara una persona que lleve 20 semanas de experiencia?