3.3 Representación gráfica de los datos
Al igual que para la construcción de las tablas de distribución de frecuencias para datos agrupados y no agrupados, la representación gráfica de las variables de estudio, dependen de la naturaleza de cada variable, esto es, de como se haya clasificado previamente, obedeciendo a esto, se presentan los siguientes tipos de gráficos. Es de resaltar que la información contenida en un gráfico es de gran ayuda para el entendimiento y análisis del conjunto de datos, y en muchos escenarios, es incluso mas pertinente que las tablas de distribución, sin que con esto se afirme que las T.D.F. no sean útiles.
3.3.1 Gráficos para variables Cualitativas
Los gráficos mas comunes, para este tipo de variable, sin importar si es nominal u ordinal, son: circular o pastel y barras.
Gráfico circular o pastel
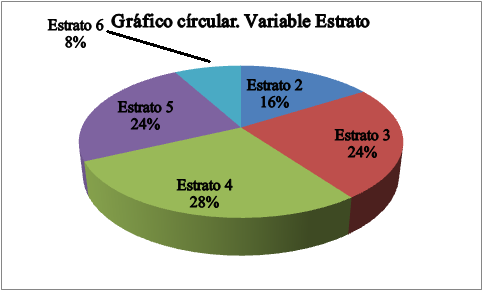
Este gráfico es un círculo dividido en porciones, cada una de las cuales corresponde a la frecuencia absoluta o a la frecuencia relativa, teniendo en cuenta que la totalidad de los datos (100%) coinciden con el círculo completo. La ilustración N°1 corresponde al gráfico circular para la variable “Estrato”, la cual concuerda con la Tabla N°3.
Con una regla de tres se pueden obtener las divisiones o porciones exactas, ya que al círculo completo (100% de los datos) le corresponden 360° y al 16% de los datos le corresponden 57.6°, de igual forma se obtienen las siguientes porciones. Concluya Usted este ejercicio y compruebe que el gráfico es el que a continuación se ilustra.
Ilustración 1: Gráfico para la variable “Estrato”.
Del gráfico anterior se puede decir: “lo mas común es encontrar clientes de la compañía de seguros, que vivan en estrato 4”.
Gráfico de barras
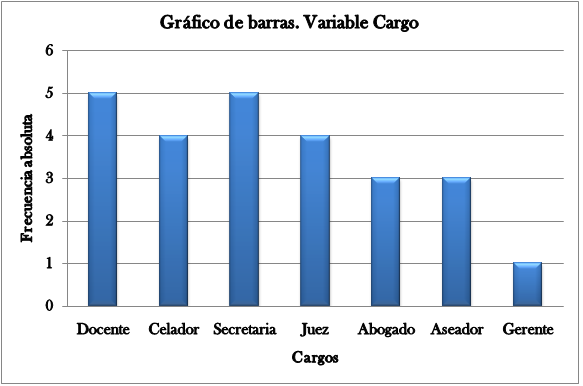
Este gráfico consiste de un conjunto de barras ya sean verticales u horizontales dispuestas en un plano cartesiano, cuya longitud depende de la frecuencia absoluta, fi o la frecuencia relativa, hi y con un ancho igual para todas pero arbitrario. En uno de los ejes se tienen las categorías de las variables y en el otro eje las frecuencias absolutas o relativas. La ilustración 2 muestra este tipo de gráfico para la variable “Cargo”.
Ilustración 2: Gráfico de barras para la variable “Cargo”
Del gráfico anterior se puede decir: “sólo un cliente de la compañía La tranquilita es gerente”.
3.2 Gráficos para las variables Cuantitativas
Cuando la variable es cuantitativa y los datos no se encuentran agrupados, los gráficos mas comunes que se utilizan son: cajas y tallos y hojas. Por el contrario, si los datos son agrupados en tabla de intervalos, los gráficos mas utilizados, en este caso son: histograma, polígono de frecuencias y ojiva.
3.2.1 Gráficos para datos agrupados
Al igual que en los gráficos ya estudiados, para variables nominales y ordinales, este tipo de gráfico se apoya en la tabla respectiva.
3.2.2 Histograma
Es un gráfico que consta de columnas consecutivas, con un ancho fijado por la amplitud de los intervalos de la tabla en la cual se basa, y cuya altura corresponde a la frecuencia absoluta o relativa. La ilustración 3, apoyada en la tabla N°4, muestra el gráfico para la variable respectiva
.
lustración 3: Histograma para la variable “salario”
Del gráfico se puede decir: “12 afiliados a la compañía de seguros ganan entre $485.068 y 1’289.809 pesos”.
3.2.3 Polígono de frecuencias
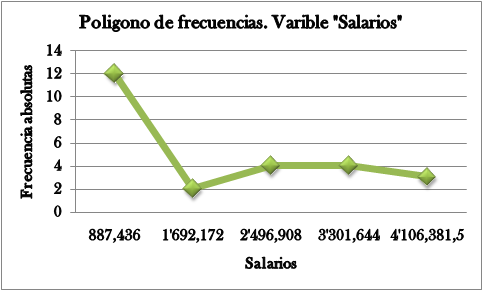
Este es un gráfico que puede obtener se del histograma, solo que ahora se consideran las marcas de clase Yi y no los intervalos. La ilustración 4, apoyada en la tabla N°5, muestra el gráfico para la variable respectiva.
Ilustración 4: Polígono de frecuencias para la variable “Salario”
Del gráfico anterior se puede decir: “12 afiliados a la compañía de seguros ganan en promedio $887.436” pesos”.
3.2.4 Ojiva
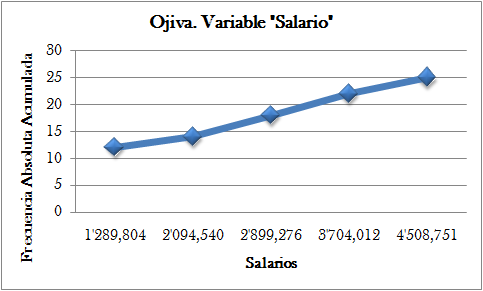
Este gráfico consiste en una linea asociada a la Frecuencia Absoluta Acumulada o a la Frecuencia Relativa Acumulada, para su construcción, se ubica en el eje horizontal los extremos superiores de cada uno de los intervalos y en el eje vertical alguno de las frecuencias ya mencionadas. La ilustración 5, apoyada en la tabla N°4, muestra el gráfico para la variable respectiva.
Ilustración 5: Ojiva para la variable “Salario”
Del gráfico anterior se puede decir: “22 afiliados a la compañía de seguros La tranquilita, ganan salarios menores o iguales a $3’704.012 pesos”.
3.2.5 Gráficos para datos no agrupados
En este caso, los datos no son tomados de ninguna TDF o tabla de intervalos, sino directamente de la matriz de datos.
3.2.6 Cajas
Es un gráfico cuya figura es una caja que encierra el 50% de los datos centrales, previamente ordenados. Antes de explicar su construcción se requiere saber que son y como se calculan cuartiles.
Cuando el conjunto de datos, previamente ordenados se dividen en cuatro partes iguales, se tienen subconjuntos del conjunto de datos llamados cuartiles Qii = 1, 2, 3, 4. Q1 o primer cuartil, hasta el cual se acumula el 25 % de los datos, Q2 o segundo cuartil, hasta el cual se acumula el 50% de los datos, Q3o tercer cuartil, hasta el cual se acumula el 75% de los datos y Q4o cuarto cuartil, hasta donde se acumula el 100% de los datos. Para hallar Q2 se divide el conjunto de datos en dos partes iguales, si el n el numero total de datos es impar, entonces Q2toma el valor del dato que esta en la mitad, esto es, en la posición, X(n + 1)/(2),y si n es par, entonces Q2toma el valor que resulta de promediar los dos datos centrales, esto es, los datos que están en las posiciones X(n)/(2) y X(n)/(2) + 1. De manera similar se calculan Q1 y Q3, teniendo cuidado de excluir para estas cuentas a Q2.
El gráfico de cajas se construye ubicando los cuartiles Q1, Q2 y Q3, sobre un eje horizontal, guardando las proporciones entre los valores de los datos, levantando lineas verticales (de altura arbitraria) sobre cada uno de estos valores y se trazan lineas horizontales para armar la caja. Se calculan enseguida, los limites inferior y superior del gráfico con formulas:
LI = Q1 − 1.5(Q3 − Q1) y LS = Q3 − 1.5(Q3 − Q1),
los datos menores y superiores a LI y LS, respectivamente, son considerados como atípicos, los cuales usualmente se denotan por puntos. Sobre estos valores limites se levantan lineas verticales de altura igual a la caja, por ultimo se ubican los valores mínimo y máximo que quedan después de excluir los valores atípicos.
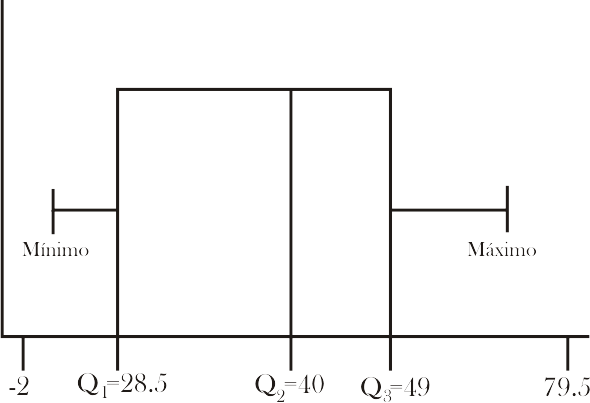
Para la variable edad, se tiene que Q1 = 28.5, Q2 = 40 y Q3 = 49, el limite inferior LI=-2, el limite superior LS=79.5, el valor mínimo es 22 y el valor máximo es 62. La ilustración 6, muestra el gráfico correspondiente, note que no existen datos atípicos entre el grupo de personas que tienen asegurada la compañía.
Ilustración 6: Gráfico de cajas para la variable “Edad”.
De este gráfico se puede decir: “lo mas usual es que los clientes de la aseguradora tengan 28.5 y 40 años”.
3.2.7 Gráfico de tallos y hojas
Es otro gráfico útil para variables cuantitativas y consiste en dividir los datos que se tienen en dos partes, la primera sera el tallo y la segunda corresponde e la hoja. Ejemplo si el dato es 45, entonces 4 sera el tallo y 5 sera la hoja; si el dato es 5.3, entonces la parte entera sera el tallo y la parte decimal sera la hoja. Para su construcción, se ubican ordenados en forma ascendente, separados por tallos y hojas todos los datos, sobre una linea vertical, a la izquierda de ella estarán los tallos y a la derecha de la misma, las hojas. Es importante tener en cuenta que solo hay una hoja por cada tallo, por lo tanto, es posible que se ignoren algunos dígitos cuando se elabore este gráfico (ejemplo si el dato es 45.357, se puede tomar 45 como tallo y 3 como hoja). Si hay datos que son muy altos o muy bajos (como datos atípicos), con respecto al conjunto de datos, entonces se especifica en la parte inferior del gráfico. En una columna a la izquierda del gráfico, se ubican las frecuencias acumuladas de arriba hacia abajo y de abajo hacia arriba, hasta donde se encuentre el 50% de los datos, el cual se representa con un paréntesis.
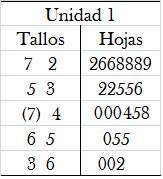
Con los datos de la variable edad, se ejemplificara el gráfico de tallos y hojas. Primero que se debe hacer es ordenar ascendente mente los datos, después definir como separar cada dato en tallos y hojas, en este caso, se tiene que las decenas serán los tallos y las unidades corresponderán a las hojas. Ordenando los datos, tenemos: 22, 26, 26, 28, 28, 28, 29, 32, 32, 35, 35, 36, 44, 45, 48, 48, 50, 55, 55, 60, 60 y 62.
Ilustración 7: Gráfico de tallos y hojas para la variable “Edad”
Del gráfico anterior, se puede decir que un 50% las personas que son clientes de la aseguradora, tienen como máxima 48 años. La unidad 1, indica que por ejemplo, 6|0 representa el dato 60.
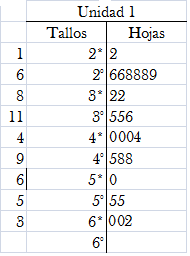
Es posible tener reforma al gráfico de tallos y hojas, cuando no se vislumbra bien las características principales del conjunto de datos. Por ejemplo, a los tallos que tienen hojas 0, 1, 2, 3, y 4 se le escribe un *, y a los tallos que tienen hojas 5, 6, 7, 8, y 9, se les escribe un °. La siguiente ilustración 8 muestra el refinamiento correspondiente al gráfico anterior.
Ilustración 8: Refinamiento del gráfico de tallos y hojas para la variable “Edad”
En algunos casos es necesario afinar aun mas el numero de tallos resultantes de la siguiente manera: para las hojas que son 0 y 1, sus tallos llevaran *, para las hojas que son 2 3 sus tallos llevaran T, para las hojas que son 4 5 sus tallos llevaran F, para las hojas que son 6 y 7 sus tallos llevaran S y para las hojas que son 8 y 9, sus tallos llevaran°.